Die Gruppe E (und auch Gruppe F mit Österreich) wird bei der EURO 2016 klar benachteiligt, die Gruppe A von Gastgeber Frankreich hingegen systematisch bevorzugt. Und das hat gar nichts mit einer unglücklichen Auslosung zu tun. Ein Report von Sebastian Wolsing zeigt die statistische Ungerechtigkeit des Turniermodus mit 24 Mannschaften, 6 Gruppen und einem Achtelfinale.

Der Gruppe E-Effekt: Gruppe E ist die schlimmste bei der Euro

1. Einleitung

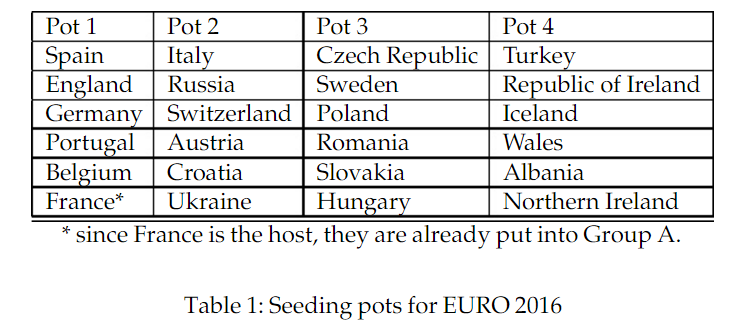
Die Europameisterschaft in Frankreich beginnt am 10. Juni 2016. Falls das Konzept von Fußballturnieren neu für dich ist, musst du nicht viel wissen: Teams qualifizieren sich und werden aus vier verschiedenen Lostöpfen gemäß ihrer Stärke in Gruppen gelost. Jede der sechs Gruppen besteht aus einer Mannschaft aus jedem Topf. Frankreich wird als Gastgeber automatisch in Gruppe A gesetzt.

2. Der Gruppe-E-Effekt

Viele von uns denken, dass es bei der Auslosung nicht wichtig ist, in welcher Gruppe man landet. Wichtig seien nur die Gegner, die man zugelost bekommt. Aber bei dieser speziellen Europameisterschaft ist das nicht richtig. Die Playoff-Struktur nach der Gruppenphase sieht nämlich so aus:

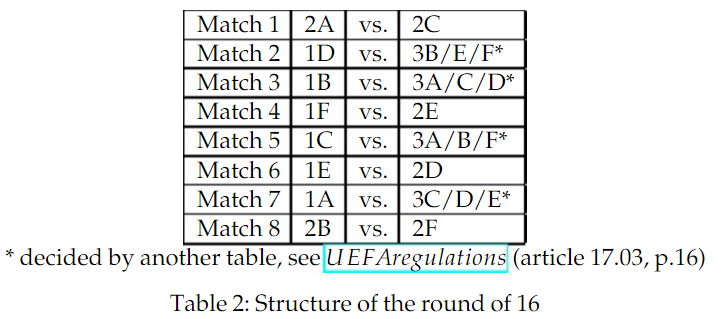
Wir haben also 6 Gruppen, Gruppensieger und Gruppenzweite. Das ergibt 12 Teams, die weiterkommen. Für die 16 nötigen im Playoff kommen noch die vier besten Gruppendritten weiter. Die mathematische Symmetrie in einem System mit vier oder acht Gruppen besteht also nicht mehr. Das bedeutet:

1. Die Sieger aus Gruppe A, B, C und D treffen im Achtelfinale auf Gruppendritte. Die Sieger aus E und F treffen auf Gruppenzweite. Eine klare Benachteiligung.
2. Die Gruppenzweiten aus A, B, C und F treffen auf andere Gruppenzweite, jene aus D und E auf einen Gruppensieger. Eine klare Benachteiligung.
3. Die Gruppen A, B und C bekommen beide Vorteile.
4. Die Gruppen D und F bekommen je einen Vor- und Nachteil.
5. Die Gruppe E bekommt beide Nachteile.

Das würde theoretisch bedeuten, dass Mannschaften aus Gruppe E im Playoff bereits eine geringere Wahrscheinlichkeit haben, ins Viertelfinale einzuziehen. Gruppe D und F haben eine höhere als E, aber eine niedrigere als A, B und C.

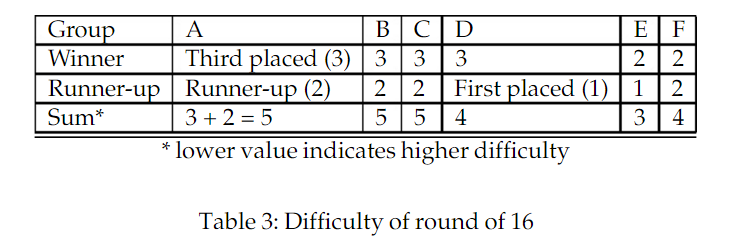
Das gilt für das Achtelfinale. Aber auch das Viertelfinale ist nicht symmetrisch. Der Sieger aus Spiel 1 und 8 im Achtelfinale wird auf jeden Fall ein Gruppenzweiter sein.

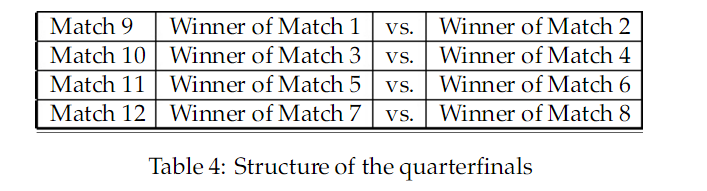
Die Sieger aus Spiel 2 und 7 treffen also automatisch nicht auf einen Ersten. Das können die Sieger aus den Gruppen A und D, oder mit niedrigerer Wahrscheinlichkeit die Drittplatzierten aus B, E, F bzw. aus C, D, E sein.

Wir erwarten hier also, dass die Gruppen A und D im Viertelfinale einen Vorteil haben werden, weil ihre Sieger bis zum Semifinale keinen anderen Gruppensieger treffen können.

Theoretisch ist also die Wahrscheinlichkeit für einen Sieg eines Teams aus Gruppe A höher, als für Mannschaften aus allen anderen Gruppen.

3. Simulationen

Mit Simulationen können wir dieses Problem noch deutlicher illustrieren. Die folgenden Simulationen wurden so gewichtet, dass das beste Team eine hohe Wahrscheinlichkeit auf einen Sieg gegen das schlechteste Team hat (Anm. von ballverliebt: Sebastian hat sein SImulationsmodell in den Kommentaren etwas genauer erklärt).

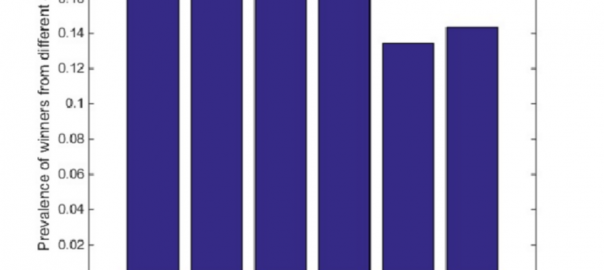
Nach 100.000 Simulationen sieht das Ergebnis für den Einzug ins Viertelfinale folgendermaßen aus.

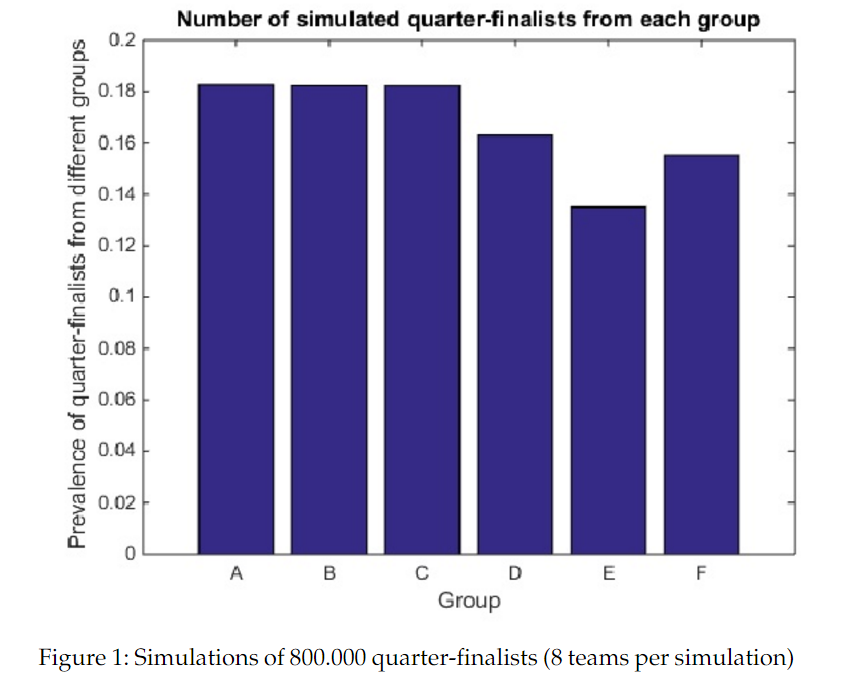
Man sieht: Gruppe E und F haben einen großen Nachteil gegebüber den anderen. A, B und C haben einen deutlich einfacheren Weg als die anderen Gruppen und E hat den schwierigsten.

Für das Semifinale sieht das Ergebnis in der Folge so aus:

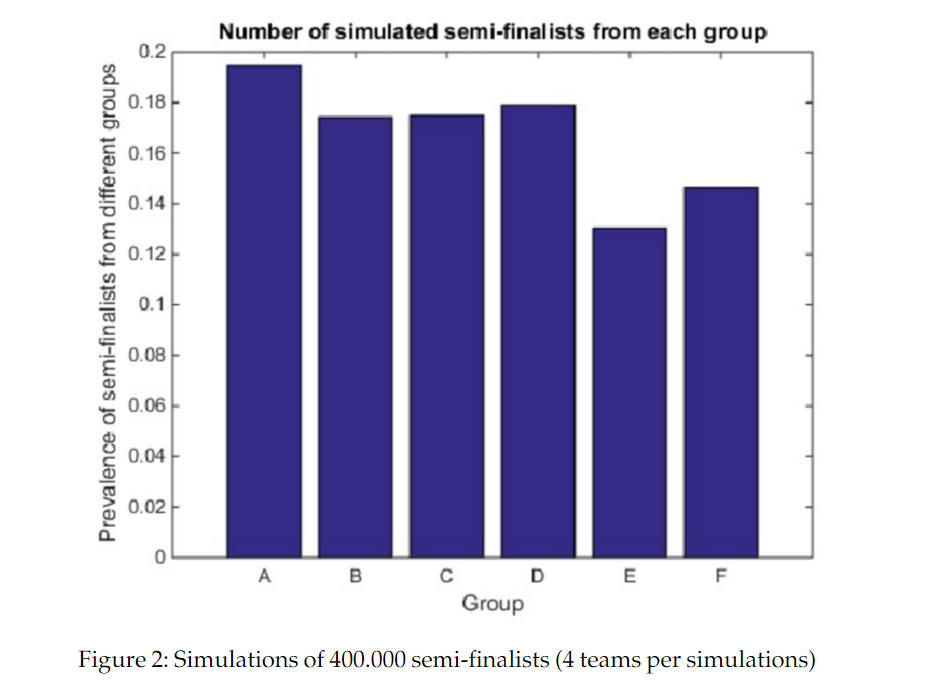
Das zeigt, dass sich die Chancen für A und D im Viertelfinale leicht erhöhen. Kommen wir zum Gewinn des Turniers.

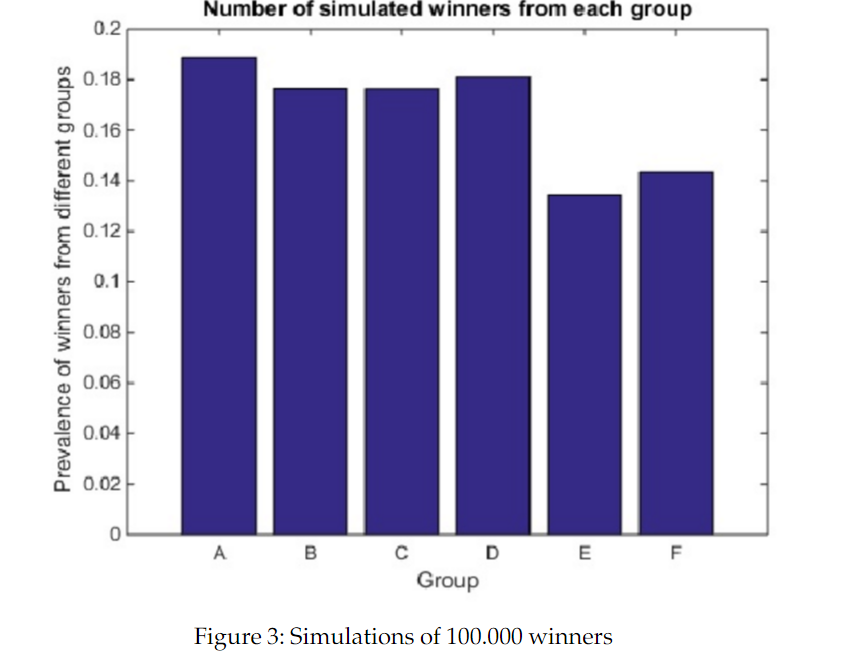
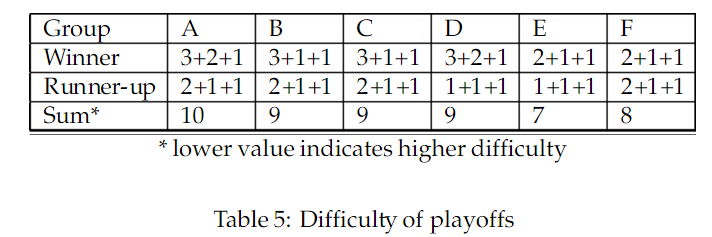
Die Simulationen bestätigen, was die Tabelle 3 bereits angedeutet hat. Die Wahrscheinlichkeit das Turnier aus den unterschiedlichen Gruppen heraus zu gewinnen. Basierend auf diesen Werten ist es 28% weniger wahrscheinlich, das Turnier aus Gruppe E zu gewinnen, als aus Gruppe A. Das scheint mir außerhalb einer fairen Schwankungsbreite zu liegen.

4. Verbesserungen

Das scheint kein optimaler Weg zu sein, um eine Europameisterschaft zu organisieren. Wie könnte man das verbessern? Es ist zwar wenig hilfreich, aber man kann argumentieren, dass ein System mit 6 Gruppen mathematisch unnütz ist. Auch 16 Aufsteiger aus 24 Mannschaften könnte man für keine gute Idee halten.

Die Dinge, die UEFA berücksichtigen will sind:

• Bedingung 1: Mannschaften aus der selben Gruppe sollen in der ersten Playoffrunde nicht aufeinander treffen.
• Bedingung 2: Der Playoff-Baum soll symmetrisch sein.

Daraus ziehen wir für die Playoffs nach der Gruppenphase folgenden Schluss. Es gibt

• Sechs Erstplatzierte (6 x 1 = 6)
• Sechs Zweitplatzierte (6 x 2 = 12)
• Vier Drittplatzierte (4 x 3 = 12)

In Summe ergibt das 30 (6 + 12 + 12), was nicht rund durch die Zahl der Spiele im Achtelfinale (8) dividiert werden kann. Bei vier Gruppen mit sechs Teams würde das anders aussehen. 4 x 1 + 4 x 2 + 4 x 3 + 4 x 4 = 40, was dividierbar durch 8 ist.

Die UEFA will das aber verzweifelt mit sechs Gruppen durchziehen, dann müssen wir aber Bedingung 1 von vorhin verwerfen. Man könnte stattdessen nach der Gruppenphase alle Aufsteiger so reihen, wie es nun mit den Gruppendritten gemacht wird und daraus das Viertelfinale gestalten.

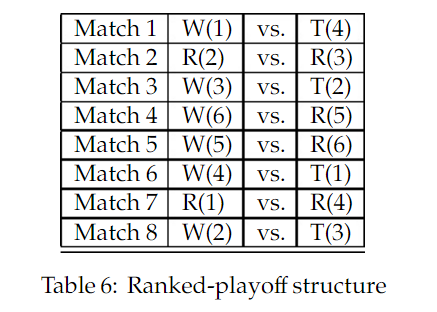
Nach dieserm Modell sehen Simulationen folgendermaßen aus:

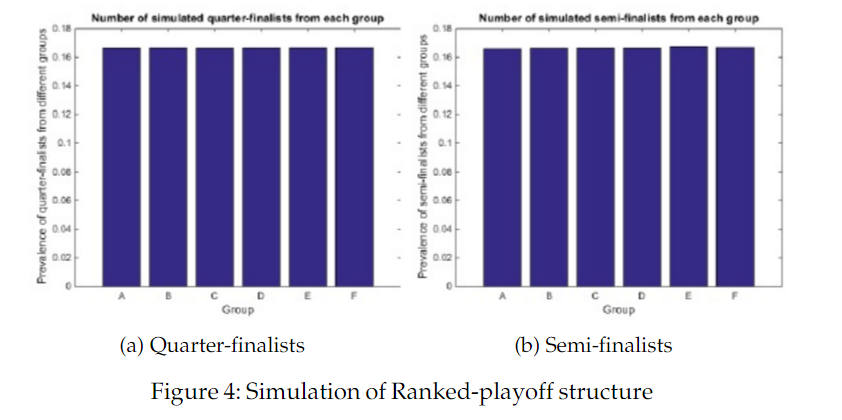
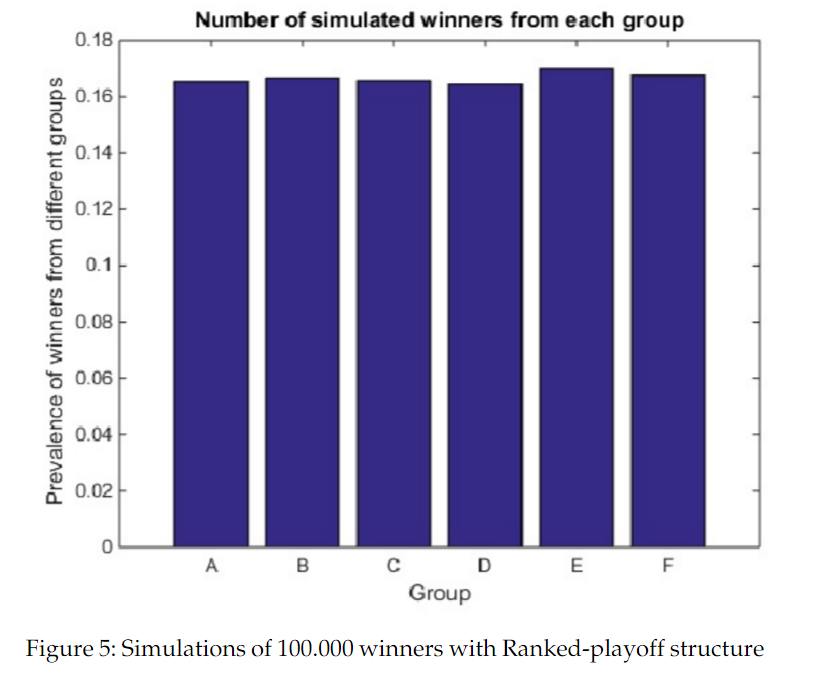
Das wäre sportlich und mathematisch fairer. Es muss aber gesagt werden, dass es für die Teams weniger praktikabel wäre. Sie wüssten vor dem Ende der kompletten Gruppenphase nicht, wo ihr nächstes Spiel stattfindet. Praktische Beschränkungen sprechen auch gegen das ansonsten beste System. Die vielen Spiele in einem Double-Elimination-System, würden zu viel kosten.

5. Schlussgedanken

Eine bemerkenswerte Sache ist, dass die „Regeln“ besagen, dass der Gastgeber in Gruppe A sein muss. Dort besteht eine höhere Chance auf den Turniergewinn. Da der Gastgeber außerdem unabhängig von seiner Ranglistenplatzierung immer in Topf 1 gesetzt wird, ist die Gruppe A noch einmal zusätzlich als absoluter Goldtopf zu sehen.

Ich werde den Teams in Gruppe E etwas fester die Daumen drücken. Sie werden es brauchen.

Mit freundlicher Genehmigung von Sebastian Wolsing durch ballverliebt.eu übersetzt.